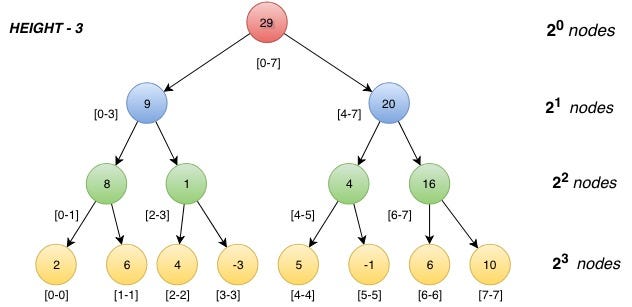
Segment Tree
A Segment Tree is a binary tree data structure that is used for efficiently answering range queries and performing updates on an array or a list. It breaks down an array into smaller segments and precomputes summary information for each segment, allowing for quick calculations and modifications within specified ranges.
Structure of a Segment Tree:
- Leaf Nodes:
- Leaf nodes of the tree represent individual elements of the array.
- Internal Nodes:
- Each internal node represents a segment of the array, and it stores precomputed information summarizing the values within that segment. Common summaries include the sum, minimum, maximum, or other aggregate values.
- Construction:
- The tree is built in a bottom-up manner. Leaf nodes are initialized with the values of the array elements, and each internal node is constructed based on the information from its children.
Range Queries and Updates:
- Query:
- To answer a range query (e.g., sum of elements in a given range), the tree efficiently combines the information stored in its nodes to provide the answer. This process has a time complexity of O(log N), where N is the number of elements in the array.
- Update:
- To perform an update (e.g., change the value of an element), the tree is modified, and affected nodes are updated accordingly. The update operation also has a time complexity of O(log N).
When to Use a Segment Tree:
Use a Segment Tree when:
- Versatility is Required:
- Segment Trees are versatile and can be adapted to various types of range queries and updates. They can efficiently handle problems involving sums, minimums, maximums, or other associative operations within a range.
- Frequent Range Queries and Updates:
- When an application involves frequent range queries and updates on an array or list, a Segment Tree provides an efficient solution.
- Logarithmic Time Complexity is Acceptable:
- The logarithmic time complexity of range queries and updates is acceptable for the size of the problem. While Segment Trees provide efficient operations, they may be overkill for very small datasets.
Example Applications:
- Sum of Elements in a Range:
- Calculate the sum of elements in a given range of an array.
- Minimum or Maximum Element in a Range:
- Find the minimum or maximum element in a specified range.
- Range Updates:
- Perform updates (addition, subtraction, etc.) on elements within a specified range efficiently.
Why Use a Segment Tree:
- Efficiency:
- Segment Trees provide efficient solutions for range queries and updates, with logarithmic time complexity.
- Versatility:
- They can be adapted to various types of problems involving ranges, making them versatile for a wide range of applications.
- Balanced Trade-Off:
- Segment Trees strike a balanced trade-off between
precomputationand query/update efficiency, making them suitable for problems with dynamic datasets and frequent operations.
- Segment Trees strike a balanced trade-off between
Comparison with Prefix Sums
- Both can have similar functionalities, such as pre-computing sums and finding range sum queries, however in this regard segment tree offer additional advantage which is performing update operation in
logntime.- In prefix sums update of an index will lead you to update all the elements thus
On
- In prefix sums update of an index will lead you to update all the elements thus
Implementation
class Node(object):
def __init__(self, start, end):
self.start = start
self.end = end
self.total = 0
self.left = None
self.right = None
class NumArray(object):
def __init__(self, nums):
self.root = self.createTree(nums, 0, len(nums)-1)
def createTree(self, nums, l, r):
#base case
if l > r:
return None
#leaf node
if l == r:
n = Node(l, r)
n.total = nums[l]
return n
mid = (l + r) // 2
root = Node(l, r)
#recursively build the Segment tree
root.left = self.createTree(nums, l, mid)
root.right = self.createTree(nums, mid+1, r)
#Total stores the sum of all leaves under root
#i.e. those elements lying between (start, end)
root.total = root.left.total + root.right.total
return root
def update(self, i, val):
return self._update(self.root, i, val)
def _update(self, root, i, val):
#Base case. The actual value will be updated in a leaf.
#The total is then propogated upwards
if root.start == root.end:
root.total = val
return val
mid = (root.start + root.end) // 2
#If the index is less than the mid, that leaf must be in the left subtree
if i <= mid:
self._update(root.left, i, val)
#Otherwise, the right subtree
else:
self._update(root.right, i, val)
#Propogate the changes after recursive call returns
root.total = root.left.total + root.right.total
return root.total
def sumRange(self, i, j):
return self._sumRange(self.root, i, j)
def _sumRange(self, root, i, j):
#If the range exactly matches the root, we already have the sum
if root.start == i and root.end == j:
return root.total
mid = (root.start + root.end) // 2
#If end of the range is less than the mid, the entire interval lies
#in the left subtree
if i <= mid: #short for = (i <= mid and mid >= j)
return self._sumRange(root.left, i, j)
#If start of the interval is greater than mid, the entire inteval lies
#in the right subtree
elif i > mid: #short for = (i > mid and mid < j)
return self._sumRange(root.right, i, j)
#Otherwise, the interval is split. So we calculate the sum recursively,
#by splitting the interval
else:
return self._sumRange(root.left, i, mid) + self._sumRange(root.right, mid+1, j)
# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(index,val)
# param_2 = obj.sumRange(left,right)